Clustering Techniques

Clustering

Cluster Analysis("dаta segmentation") is an exploratory method for identifying homogenous groups ("clusters") of records

• Similar records should belong to the same cluster
• Dissimilar records should belong to different clusters
• In Clustering there are two types of Clusters they are:
  • Hierarchical Clustering
  • Non-Hierarchical Clustering

Hierarchical Clustering Alogorithm:

• Hierarchical methods-agglomeratives: Begin with n clusters; sequentially merge similar clusters until 1 cluster is left. Useful when goal is to arrange the clusters into a natural hierarchy. Requires specifying distance measure

Clustering

Cluster Analysis(“dаta segmentation”) is an exploratory method for identifying  homogeneous groups
(“clusters”) of records

• Similar records should belongs to same cluster
• Dissimilar records should belongs to different clusters
• In clustering there are two types of clusters they are:
  • Hierarchical clustering
  • Non-Hierarchical clustering

Hierarchical clustering Algorithm:

• Hierarchical methods - Agglomerative

Begin with n clusters;sequentially merge similar clusters until 1 cluster is left.
Useful when the goal is to arrange the clusters into natural hierarchy.
Requires specifying distance measures

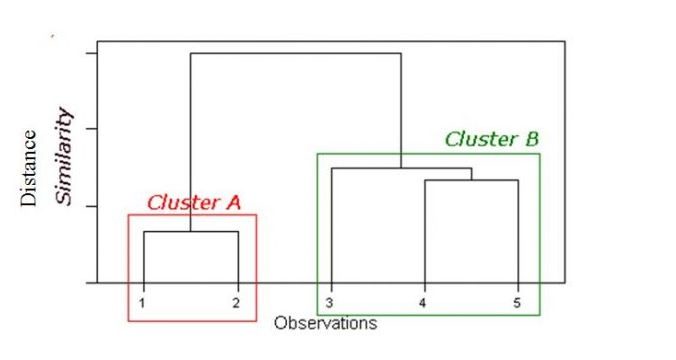
Dendrogram:

Tree like diagram that summarise the clustering process
Similar records join by links
Record location determined by similarity to other records

• Start with n clusters

( 1 record in each cluster)

• Step 1: Two closest records merged into one cluster
• At every step, pairs of records/clusters with smallest distance are merged.

- Two records are merged,
- or single record added to the existing cluster,
- or two existing clusters are combined
- requires a definition of distance.

Pairwise distance between records:  

         
dij = distance between records i and j
Distance requirements : Non-negative(dij>0) dii =0
Symmetry(dij = dji)
Triangle inequality (dij+djk>=djk)

Distance for  binary dаta

• Binary Euclidean Distance : (b+c) / (a+b+c+d)
• Simple matching coefficient : (a+d) / (a+b+c+d)
• Jaquard’s coefficient : d / (b+c+d)

for>2 categories,distance=0 only if both items have same category.Otherwise=1

Distances for mixed(Numerical+categorical)Dаta

• Simple:Standardized numerical variables to [0,1],the use euclidean distance for all
• Gower’s general dissimilarity coefficient

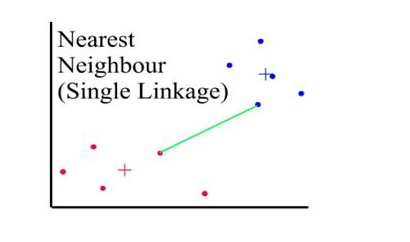
Distances between clusters: ;’Single linkage’(‘nearest neighbour’)

• Distance between 2 clusters = minimum distance between members of the two clusters

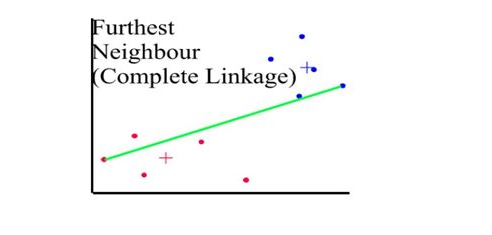
Distances between clusters: ;’complete linkage’(‘farthest neighbour’)

• Distance between 2 clusters = Greatest distance between members of the two clusters

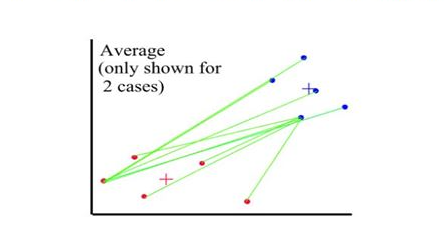
Distances between clusters: ; ‘Average linkage’

• Distance between 2 clusters = Average of all distances between members of the two clusters

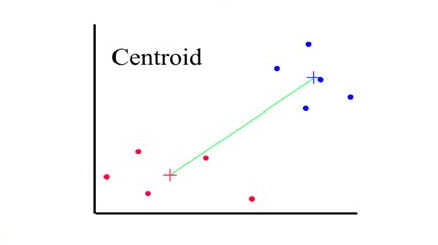
Distances between clusters: ; ‘Centroid linkage’

• Distance between 2 clusters = Distance between centroids(centers)

Hierarchical
The good

• Finds “natural” grouping - no need to specify number of clusters
• Dendrogram: transparency of process, good for presentation

The Bad

• Require computation and storage of n/n distance matrix
• Algorithm makes only one pass through the dаta.records that are incorrectly allocated early on cannot be reallocated subsequently
• Low stability : recording dаta or dropping a few records can leads to different solution
• single complete linkage robust to distance metrics as long as the relative ordering is kept .
• Average linkage is Not.
• Most distances sensitive to outliers.

Non-Hierarchical methods:
K-means clustering

• pre-specified number of clusters ,assign records to each of the clusters.
• Requires specifying # clusters
• Computationally cheap
• Predetermined number(k) of non-overlapping clusters
• Clusters are homogenous yet dissimilar to other clusters
• Need measures of within-cluster similarity(homogeneity) and between-cluster similarity
• No hierarchy(no dendrogram)!End-product is final cluster memberships
• Useful for large dаtasets

Algorithm minimizes within-cluster variance(heterogeneity)

1.For a user-specified value of k,partition dаtaset into k initial clusters
2.For each record,assign it to cluster with closest centroid
3.Re-calculate centroids for the “losing” and “receiving” clusters.Can be done

• After reassignment of each record,or
• After one complete pass through all records(cheaper)        

4.Repeat step 2-3 until no more assignment is necessary

Initial partition into k clusters
Initial partitions can be obtained by either

1. User-specified initial partitions,or
2. User-specified initial centroids,or
3. Random partitions

Stability : run algorithm with different initial partitions
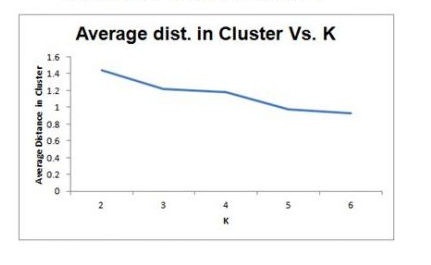
Selecting K

• Re-run algorithm for different values of k
• Trade off: simplicity (interpretation) vs.adequacy ( within-cluster homogeneity)
• Plot within-cluster variability as a function of k

K-Means
The Good                                                           

• Computationally fast for large dаtasets
• Useful when certain k needed

The Bad 

• Can take long to terminate
• Final solution not guaranteed to be  “globally optimal”
• Different  initial partitions can lead to different solutions
• Must re-run the algorithm for different values of K No dendrogram