Correlation and Covariance are two commonly used statistical concepts majorly used to measure the linear relation between two variables in data. When used to compare samples from different populations, covariance is used to identify how two variables vary together whereas correlation is used to determine how change in one variable is affecting the change in another variable. Even though there are certain similarities between these two mathematical terms, these two are different from each other. Read further to understand the difference between covariance and correlation.
Covariance:
It is an indicator of the degree to which two variables change with respect to each other i.e.., it measures the direction of linear relationship between these two variables .The values of covariance can lies in the range of -? to +?

Here,
- Xi – values of X variable
- yj – values of Y variable
- X?- mean of x variable
- Y?- mean of y variable
- N- Number of data points ( n-1 for sample covariance)
Now let’s see how to calculate the same in python using inbuilt functions:


Here, Covariance for the variable itself is the variance for the same.
Correlation:
Correlation measures the strength and direction of linear relationship between two variables or we can say it’s a normalized version of covariance. By dividing the covariance with standard deviation of the variables it scales down the range to -1 to +1 , comparatively correlation values are more interpretable.



As we can see from the formula itself, correlation is calculated from standardising covariance results; let us just execute the same in python and see the difference.


Here , the correlation results on original data is similar to covariance on standardized data ( with deviation in decimal values ) . For any of our applications like PCA , we can use either of them which yields the same results. Alternatively, we can use function from NumPy modules as well Covariance : numpy.cov(a,b) Correlation: numpy. corrcoef (a,b)
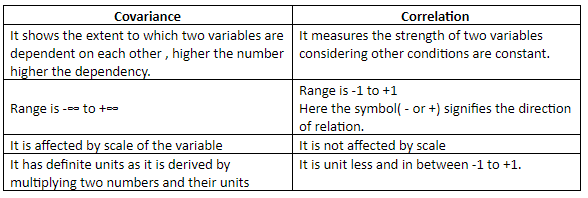
Difference between Correlation and Covariance:
Covariance is affected by the change in scale as opposite to the same correlation values are not influenced by change in scale. Correlation values are dimensionless with unit free and scale free measure of strength and direction between two variables.
Conclusion:
Both covariance and correlation are closely related to each other and differ a lot when it comes to making a choice between these two. Most of the analysts prefer correlation as it is more interpretable and will not be affected by scale and units in the data.